Johannes Kepler (1571 to 1630) fue un matemático y astronomo alemán que descubrio que la tierra y los planetas giran alrededor del sol en orbitas elipticas. Formuló las tres leyes fundamentales del movimiento de los planetas y realizó importante trabajo en óptica y en geometría.
La ciencia
para Johannes Kepler es una mirada de lo matemático/geométrico fundamentada en
lo religioso para explicar desde estas tres perspectivas como son los movimientos de los planetas, el
papel de los cuerpos celestes dentro del mismo, las proporciones y posiciones
de los mismos en el sistema solar.
Johannes Kepler es uno de los representantes más significativos de la llamada revolución científica de los siglos 16 y 17. A pesar de que recibió sólo la formación básica de un "magister" y se orientó profesionalmente hacia la teología en el comienzo de su carrera, él rápidamente se hizo conocido por sus habilidades matemáticas y la creatividad teórica.
Como copernicano convencido, Kepler fue capaz de defender el nuevo sistema en diferentes frentes: contra los antiguos astrónomos que todavía sostenían el sistema de Ptolomeo, en contra de los filósofos de la naturaleza aristotélica, en contra de los seguidores de la nueva "sistema mixto" de Tycho Brahe, a quien Kepler sucedió como Matemático Imperial en Praga, e incluso en contra de la posición copernicana norma según la cual el nuevo sistema debía considerarse simplemente como un dispositivo de cómputo y no necesariamente una realidad física.
El Corpus completo de Kepler puede apenas resumir como un "sistema" de ideas como la filosofía escolástica o los nuevos sistemas cartesianos que surgieron en la segunda mitad del siglo 17. Sin embargo, es posible identificar dos tendencias principales, uno vinculado al platonismo y dando prioridad a la función de la geometría de la estructura del mundo, el otro conectado con la tradición aristotélica y acentuando el papel de la experiencia y de la causalidad en la epistemología.
Mientras que alcanzó la fama inmortal en la astronomía, debido a sus tres leyes planetarias, Kepler también hizo contribuciones fundamentales en los campos de la óptica y matemáticas. A los hechos poco conocidos sobre la actividad científica infatigable de Kepler pertenecen a sus esfuerzos para desarrollar diferentes dispositivos técnicos, por ejemplo, una bomba de agua, el que trató de patentes y se aplican en diferentes contextos prácticos (para los documentos, consulte KGW 21.2.2., pp. 509-57 y 667-691).
Para sus contemporáneos él también fue un famoso matemático y astrólogo; por su parte, quería ser considerado un filósofo que investigó la estructura íntima del cosmos científicamente.
Johannes Kepler es uno de los representantes más significativos de la llamada revolución científica de los siglos 16 y 17. A pesar de que recibió sólo la formación básica de un "magister" y se orientó profesionalmente hacia la teología en el comienzo de su carrera, él rápidamente se hizo conocido por sus habilidades matemáticas y la creatividad teórica.
Como copernicano convencido, Kepler fue capaz de defender el nuevo sistema en diferentes frentes: contra los antiguos astrónomos que todavía sostenían el sistema de Ptolomeo, en contra de los filósofos de la naturaleza aristotélica, en contra de los seguidores de la nueva "sistema mixto" de Tycho Brahe, a quien Kepler sucedió como Matemático Imperial en Praga, e incluso en contra de la posición copernicana norma según la cual el nuevo sistema debía considerarse simplemente como un dispositivo de cómputo y no necesariamente una realidad física.
El Corpus completo de Kepler puede apenas resumir como un "sistema" de ideas como la filosofía escolástica o los nuevos sistemas cartesianos que surgieron en la segunda mitad del siglo 17. Sin embargo, es posible identificar dos tendencias principales, uno vinculado al platonismo y dando prioridad a la función de la geometría de la estructura del mundo, el otro conectado con la tradición aristotélica y acentuando el papel de la experiencia y de la causalidad en la epistemología.
Mientras que alcanzó la fama inmortal en la astronomía, debido a sus tres leyes planetarias, Kepler también hizo contribuciones fundamentales en los campos de la óptica y matemáticas. A los hechos poco conocidos sobre la actividad científica infatigable de Kepler pertenecen a sus esfuerzos para desarrollar diferentes dispositivos técnicos, por ejemplo, una bomba de agua, el que trató de patentes y se aplican en diferentes contextos prácticos (para los documentos, consulte KGW 21.2.2., pp. 509-57 y 667-691).
Para sus contemporáneos él también fue un famoso matemático y astrólogo; por su parte, quería ser considerado un filósofo que investigó la estructura íntima del cosmos científicamente.
Johannes Kepler : Notas sobre su obra científica
Modelo platónico del Sistema solar presentado por Kepler en su obra Misterium Cosmographicum (1596).
Después de estudiar teología en la universidad de Tubinga, incluyendo astronomía, seguidor de Copérnico,
enseñó en el seminario de Graz. Kepler intentó comprender
las leyes del movimiento planetario durante la mayor parte de su vida.
En un principio Kepler consideró que el movimiento de los planetas debía
cumplir las leyes pitagóricas de la armonía. Esta teoría es conocida
como la música o la armonía de las esferas celestes. En su visión cosmológica no era casualidad que el número de planetas conocidos en su época fuera uno más que el número de poliedros perfectos.
Siendo un firme partidario del modelo copernicano, intentó demostrar que las distancias de los planetas al Sol venían dadas por esferas en el interior de poliedros perfectos, anidadas sucesivamente unas en el interior de otras. En la esfera interior estaba Mercurio mientras que los otros cinco planetas (Venus, Tierra, Marte, Júpiter y Saturno) estarían situados en el interior de los cinco sólidos platónicos correspondientes también a los cinco elementos clásicos.
Siendo un firme partidario del modelo copernicano, intentó demostrar que las distancias de los planetas al Sol venían dadas por esferas en el interior de poliedros perfectos, anidadas sucesivamente unas en el interior de otras. En la esfera interior estaba Mercurio mientras que los otros cinco planetas (Venus, Tierra, Marte, Júpiter y Saturno) estarían situados en el interior de los cinco sólidos platónicos correspondientes también a los cinco elementos clásicos.
En 1596 Kepler escribió un libro en el que exponía sus ideas. Mysterium Cosmographicum (El misterio cósmico).
Siendo un hombre de gran vocación religiosa, Kepler veía en su modelo
cosmológico una celebración de la existencia, sabiduría y elegancia de
Dios. Escribió: «yo deseaba ser teólogo; pero ahora me doy cuenta gracias a mi esfuerzo de que Dios puede ser celebrado también por la astronomía».
En 1600 acepta la propuesta de colaboración del astrónomo imperial Tycho Brahe,
que a la sazón había montado el mejor centro de observación astronómica
de esa época. Tycho Brahe disponía de los que entonces eran los mejores
datos de observaciones planetarias pero la relación entre ambos fue
compleja y marcada por la desconfianza. Hasta 1602, a la muerte de
Tycho, Kepler no consiguió tener acceso a todos los datos recopilados
por Tycho, mucho más precisos que los manejados por Copérnico.
A la
vista de los datos, especialmente los relativos al movimiento retrógrado
de Marte
se dio cuenta de que el movimiento de los planetas no podía ser
explicado por su modelo de poliedros perfectos y armonía de esferas.
Kepler, hombre profundamente religioso, incapaz de aceptar que Dios no
hubiera dispuesto que los planetas describieran figuras geométricas
simples, se dedicó con tesón ilimitado a probar con toda suerte de
combinaciones de círculos. Cuando se convenció de la imposibilidad de
lograrlo con círculos, usó óvalos.
Al fracasar también con ellos, «sólo
me quedó una carreta de estiércol» y empleó elipses. Con ellas
desentrañó sus famosas tres leyes (publicadas en 1609 en su obra Astronomia Nova)
que describen el movimiento de los planetas. Leyes que asombraron al
mundo, le revelaron como el mejor astrónomo de su época, aunque él no
dejó de vivir como un cierto fracaso de su primigenia intuición de
simplicidad (¿por qué elipses, habiendo círculos?). Sin embargo, tres
siglos después, su intuición se vio confirmada cuando Einstein mostró en su Teoría de la Relatividad general
que en la geometría tetradimensional del espacio-tiempo los cuerpos
celestes siguen líneas rectas. Y es que aún había una figura más simple
que el círculo: la recta.
Mapa del mundo, de Tabulae Rudolphine.
En 1627 publicó las Tabulae Rudolphine, a las que dedicó un
enorme esfuerzo, y que durante más de un siglo se usaron en todo el
mundo para calcular las posiciones de los planetas y las estrellas.
Utilizando las leyes del movimiento planetario fue capaz de predecir
satisfactoriamente el tránsito de Venus del año 1631 con lo que su teoría quedó confirmada.
Escribió un biógrafo de la época con admiración, lo grande y
magnífica que fue la obra de Kepler, pero al final se lamentaba de que
un hombre de su sabiduría, en la última etapa de su vida, tuviese
demencia senil, llegando incluso a afirmar que "las mareas
venían motivadas por una atracción que la luna ejercía sobre los
mares...", un hecho que fue demostrado años después de su muerte.
En su honor una cadena montañosa del satélite marciano Fobos fue bautizada con el nombre de 'Kepler Dorsum'.
Primer modelo cosmológico de Kepler (1596)
En lugar de los siete planetas en la astronomía geocéntrica estándar, en el sistema copernicano había sólo seis, la Luna Kepler la llamo a un "satélite" (un nombre que acuñó en 1610 para describir las lunas que Galileo había descubierto y que estaban orbitando Júpiter.
Por otra parte, en la astronomía geocéntrica no había manera de utilizar las observaciones para encontrar los tamaños relativos de las órbitas planetarias; que se supone que simplemente estaban en contacto. Esto parecía no requerir ninguna explicación, ya que encajaba muy bien con los filósofos naturales "creencia de que todo el sistema se convirtió en el movimiento de la esfera exterior, una (o quizás dos) más allá de la esfera de las estrellas fijas '' (aquellos cuyos patrón hecho las constelaciones), más allá de la esfera de Saturno.
En el sistema de Copérnico, el hecho de que el componente anual de cada movimiento planetario fue un reflejo del movimiento anual de la Tierra permitió que se debería usar observaciones para calcular el tamaño de la trayectoria de cada planeta, y resultó que había enormes espacios entre el planetas.
La respuesta de Kepler a estas preguntas, que se describe en su Misterio del Cosmos (cosmographicum Mysterium, Tübingen, 1596), parece extraña a lectores del siglo veinte. Sugirió que si una esfera fueron colocada en el interior de la trayectoria de Saturno, y un cubo se inscribe en la esfera, entonces la esfera inscrita en ese cubo sería la esfera que circunscribe la trayectoria de Júpiter. Entonces, si un tetraedro regular se dibuja en la esfera para inscribir la trayectoria de Júpiter, la insesphera del tetraedro sería la esfera que circunscribe la trayectoria de Marte, y así hacia el interior, poniendo el dodecaedro regular entre Marte y la Tierra, el icosaedro regular entre la Tierra y Venus y el octaedro regular entre Venus y Mercurio.
Esto explica el número de planetas perfectamente: sólo hay cinco sólidos regulares convexos (como se demuestra en los Elementos de Euclides, libro 13). También da un ajuste convincente con los tamaños de los caminos como deduce Copérnico, el mayor error es menor que 10% (que es espectacularmente bueno para un modelo cosmológico incluso ahora). Kepler no se expresa en términos de errores porcentuales, y su es decir, de hecho, es el primer modelo cosmológico matemático.
Kepler vio su teoría cosmológica como medio para proporcionar evidencia de la teoría de Copérnico. Antes de presentar su propia teoría que dio argumentos para establecer la credibilidad de la propia teoría de Copérnico. Kepler afirma que sus ventajas sobre la teoría geocéntrica están en su mayor poder explicativo. Por ejemplo, la teoría copernicana puede explicar por qué Venus y Mercurio nunca se ven muy lejos del Sol (que se encuentran entre la Tierra y el Sol), mientras que en la teoría geocéntrica no hay explicación de este hecho. Kepler enumera nueve tales preguntas en el primer capítulo de la cosmographicum Mysterium.
Kepler lleva a cabo este trabajo mientras enseñaba en Graz, pero el libro sale la prensa en Tübingen. El acuerdo con los valores deducidos de la observación no era exacta, y Kepler esperaba que mejores observaciones mejorarían el acuerdo, por lo que envió una copia de la cosmographicum Mysterium a uno de los astrónomos observacionales más destacados de la época, Tycho Brahe (1546-1601). Tycho, que entonces trabajaba en Praga (en ese momento la capital del Sacro Imperio Romano), de hecho, había ya escrito a Mästlin en busca de un asistente matemático. Kepler consiguió el trabajo.
La "Guerra con Marte '
Naturalmente, las prioridades de Tycho no eran las mismos que Kepler, y Kepler pronto se encontró trabajando en el problema insoluble de la órbita de Marte. Él continuó trabajando en esto después de que Tycho murió (en 1601) y Kepler le sucedió como Matemático Imperial. Convencionalmente, las órbitas se consideraron como círculos, y se necesitaban más bien pocos valores observacionales para fijar los radios relativos y posiciones de los círculos. Tycho había hecho una gran cantidad de observaciones y Kepler decidido a hacer el mejor uso posible de ellas. En esencia, él tenía tantas observaciones disponibles que una vez que él había construido una órbita posible pudo comprobarlo contra nuevas observaciones hasta que se llegó a un acuerdo satisfactorio.
Kepler concluyó que la órbita de Marte era una elipse con el Sol en uno de sus focos (un resultado que cuando se extiende a todos los planetas que ahora se llama "Primera Ley de Kepler"), y que la línea que une el planeta al Sol barrido áreas iguales en tiempos iguales como el planeta describen su órbita ("Segunda Ley de Kepler"), que es el área que se utiliza como una medida de tiempo. Después de que este trabajo fue publicado en Nueva Astronomía ... (Astronomia nova, ..., Heidelberg, 1609), Kepler encontró las órbitas de los otros planetas, estableciendo así las dos leyes para ellos también. Ambas leyes se refieren al movimiento del planeta al Sol; el Copernicanismo de Kepler fue crucial para su razonamiento ya sus deducciones.
El proceso real de cálculo para Marte fue inmensamente laborioso - hay cerca de mil hojas en el folio de la aritmética - y el propio Kepler se refiere a esta obra como "mi guerra con Marte ', pero el resultado fue una órbita que está de acuerdo con los resultados modernos tan exactamente que la comparación tiene que tomar en cuenta los cambios seculares en la órbita desde la época de Kepler.
Error observacional
Era fundamental el método de comprobación de las posibles órbitas con las observaciones que tienen da una idea de lo que debería ser aceptado como un acuerdo adecuado de Kepler. De esto surge el primer uso explícito del concepto de error de observación. Kepler pudo haber adeudado esta noción, al menos en parte a Tycho, que hizo los controles detallados sobre el rendimiento de sus instrumentos (véase la biografía de Brahe).
Óptica, y la nueva estrella de 1604
El trabajo sobre Marte se completó esencialmente por 1605, pero hubo demoras en el libro publicado. Mientras tanto, en respuesta a las preocupaciones acerca del diferente diámetro aparente de la Luna cuando se observa directamente y cuando se observa el uso de una cámara oscura, Kepler hizo algunos trabajos sobre óptica, y se le ocurrió la primera teoría matemática correcta de la cámara oscura y la primera explicación correcta del funcionamiento del ojo humano, con una imagen invertida formada en la retina. Estos resultados fueron publicados en suplementos, en la parte óptica de la astronomía (Ad Vitellionem paralipomena, quibus Astronomiae pars traditur optica, Frankfurt, 1604).
También escribió sobre la Nueva Estrella de 1604, ahora generalmente llamada 'supernova de Kepler', rechazando numerosas explicaciones, y comentando en un punto que por supuesto esta estrella podría ser sólo una creación especial ' (En la nueva estrella, De stella nova, Praga, 1606, Capítulo 22, KGW 1, p. 257, línea 23).
Tras el uso de Galileo del telescopio en el descubrimiento de las lunas de Júpiter, publicado en su Mensajero Sideral (Venecia, 1610), a la que Kepler había escrito una respuesta entusiasta (1610), Kepler escribió un estudio de las propiedades de las lentes (el primer tipo de trabajo sobre óptica) en la que presentó un nuevo diseño de telescopio, usando dos lentes convexas (Dioptrice, Praga, 1611). Este diseño, en el que se invierte la imagen final, tuvo tanto éxito que ahora se conoce generalmente no como un telescopio Kepler sino simplemente como el telescopio astronómico.
Dejando a Praga para Linz
Los años de Kepler en Praga fueron relativamente pacífica, y científicamente muy productivos. De hecho, incluso cuando las cosas iban mal, nunca parece haber permitido que las circunstancias externas para impedirle seguir adelante con su trabajo. Las cosas empezaron a ir muy mal a finales de 1611. Kepler tuvo que abandonar Praga. Él y el resto de sus hijos se trasladaron a Linz (ahora en Austria).
Matrimonio y los barriles de vino
Kepler parece haberse casado con su primera esposa, Barbara, por amor (aunque el matrimonio fue arreglado a través de un intermediario). El segundo matrimonio, en 1613, era una cuestión de necesidad práctica; que necesitaba a alguien para cuidar a los niños. La nueva esposa de Kepler, Susana, tuvo un curso intensivo en el carácter de Kepler: la carta dedicatoria del libro resultante explica que en las celebraciones de la boda, Kepler se dio cuenta de que se requeria estimar los volúmenes de los barriles de vino y comenzó a preguntarse cómo podría funcionar.
El resultado fue un estudio de los volúmenes de sólidos de revolución (Nueva Stereometry de barriles de vino ..., Nova stereometria doliorum ..., Linz, 1615) en la que Kepler, basándose en el trabajo de Arquímedes, usó una resolución en ' indivisibles ". Este método fue desarrollado posteriormente por Bonaventura Cavalieri (c 1598 -. 1647) y es parte de la ascendencia del cálculo infinitesimal.
La armonía del mundo.
La principal tarea de Kepler como Matemático Imperial era escribir tablas astronómicas, con base en las observaciones de Tycho, pero lo que realmente quería hacer era escribir La Armonía del Mundo, prevista desde 1599 como un desarrollo de su Misterio del Cosmos. Este segundo trabajo sobre la cosmología (libri Harmonices mundi V, Linz, 1619) presenta un modelo matemático más elaborado que el anterior, aunque los poliedros están todavía allí.
Las matemáticas en este trabajo incluyen el primer tratamiento sistemático de mosaicos, una prueba de que hay sólo trece poliedros convexos uniformes (los sólidos de Arquímedes) y el primer relato de dos poliedros regulares no convexos (todos en el Libro 2). La Armonía del Mundo también contiene lo que ahora se conoce como "la tercera ley de Kepler, que para dos planetas la relación de los cuadrados de sus periodos será la misma que la relación de los cubos de los radios medios de sus órbitas.
Juicio por Brujería
Mientras que Kepler estaba trabajando en su Armonía del Mundo, su madre fue acusada de brujería. Se contó con la ayuda de la facultad legal de Tübingen. Katharina Kepler fue finalmente puesto en libertad, al menos en parte, como resultado de objeciones técnicas derivadas de la insuficiencia de las autoridades a seguir los procedimientos legales correctos en el uso de la tortura. Los documentos que sobreviven son escalofriantes. Sin embargo, Kepler continuó trabajando. En el coche, en su viaje a Württemberg para defender a su madre, que leyó un trabajo sobre teoría de la música de Vincenzo Galilei (c.1520 - 1591, el padre de Galileo), a la que hay numerosas referencias en La Armonía del Mundo.
Tablas Astronómicas
Cálculo de las tablas, el negocio normal para un astrónomo, siempre involucrado aritmética pesado. Kepler fue consecuencia encantado cuando en 1616 se encontró con la obra de Napier sobre logaritmos (publicada en 1614). Sin embargo, Mästlin le dijo rápidamente primero que era indecoroso para un matemático serio regocijarse sobre una mera ayuda para el cálculo y la segunda que era prudente confiar en los logaritmos porque nadie entendía cómo funcionaban.
Wallenstein
En el momento en que las tablas de Rudolphine se publicaron Kepler, de hecho, ya no trabajaba para el emperador (que había dejado Linz en 1626), pero con Albrecht von Wallenstein (1583-1632), uno de los pocos líderes militares exitosos en la Trigésima Guerra Años (1618-1648).
Primer modelo cosmológico de Kepler (1596)
En lugar de los siete planetas en la astronomía geocéntrica estándar, en el sistema copernicano había sólo seis, la Luna Kepler la llamo a un "satélite" (un nombre que acuñó en 1610 para describir las lunas que Galileo había descubierto y que estaban orbitando Júpiter.
Por otra parte, en la astronomía geocéntrica no había manera de utilizar las observaciones para encontrar los tamaños relativos de las órbitas planetarias; que se supone que simplemente estaban en contacto. Esto parecía no requerir ninguna explicación, ya que encajaba muy bien con los filósofos naturales "creencia de que todo el sistema se convirtió en el movimiento de la esfera exterior, una (o quizás dos) más allá de la esfera de las estrellas fijas '' (aquellos cuyos patrón hecho las constelaciones), más allá de la esfera de Saturno.
En el sistema de Copérnico, el hecho de que el componente anual de cada movimiento planetario fue un reflejo del movimiento anual de la Tierra permitió que se debería usar observaciones para calcular el tamaño de la trayectoria de cada planeta, y resultó que había enormes espacios entre el planetas.
La respuesta de Kepler a estas preguntas, que se describe en su Misterio del Cosmos (cosmographicum Mysterium, Tübingen, 1596), parece extraña a lectores del siglo veinte. Sugirió que si una esfera fueron colocada en el interior de la trayectoria de Saturno, y un cubo se inscribe en la esfera, entonces la esfera inscrita en ese cubo sería la esfera que circunscribe la trayectoria de Júpiter. Entonces, si un tetraedro regular se dibuja en la esfera para inscribir la trayectoria de Júpiter, la insesphera del tetraedro sería la esfera que circunscribe la trayectoria de Marte, y así hacia el interior, poniendo el dodecaedro regular entre Marte y la Tierra, el icosaedro regular entre la Tierra y Venus y el octaedro regular entre Venus y Mercurio.
Esto explica el número de planetas perfectamente: sólo hay cinco sólidos regulares convexos (como se demuestra en los Elementos de Euclides, libro 13). También da un ajuste convincente con los tamaños de los caminos como deduce Copérnico, el mayor error es menor que 10% (que es espectacularmente bueno para un modelo cosmológico incluso ahora). Kepler no se expresa en términos de errores porcentuales, y su es decir, de hecho, es el primer modelo cosmológico matemático.
Kepler vio su teoría cosmológica como medio para proporcionar evidencia de la teoría de Copérnico. Antes de presentar su propia teoría que dio argumentos para establecer la credibilidad de la propia teoría de Copérnico. Kepler afirma que sus ventajas sobre la teoría geocéntrica están en su mayor poder explicativo. Por ejemplo, la teoría copernicana puede explicar por qué Venus y Mercurio nunca se ven muy lejos del Sol (que se encuentran entre la Tierra y el Sol), mientras que en la teoría geocéntrica no hay explicación de este hecho. Kepler enumera nueve tales preguntas en el primer capítulo de la cosmographicum Mysterium.
Kepler lleva a cabo este trabajo mientras enseñaba en Graz, pero el libro sale la prensa en Tübingen. El acuerdo con los valores deducidos de la observación no era exacta, y Kepler esperaba que mejores observaciones mejorarían el acuerdo, por lo que envió una copia de la cosmographicum Mysterium a uno de los astrónomos observacionales más destacados de la época, Tycho Brahe (1546-1601). Tycho, que entonces trabajaba en Praga (en ese momento la capital del Sacro Imperio Romano), de hecho, había ya escrito a Mästlin en busca de un asistente matemático. Kepler consiguió el trabajo.
La "Guerra con Marte '
Naturalmente, las prioridades de Tycho no eran las mismos que Kepler, y Kepler pronto se encontró trabajando en el problema insoluble de la órbita de Marte. Él continuó trabajando en esto después de que Tycho murió (en 1601) y Kepler le sucedió como Matemático Imperial. Convencionalmente, las órbitas se consideraron como círculos, y se necesitaban más bien pocos valores observacionales para fijar los radios relativos y posiciones de los círculos. Tycho había hecho una gran cantidad de observaciones y Kepler decidido a hacer el mejor uso posible de ellas. En esencia, él tenía tantas observaciones disponibles que una vez que él había construido una órbita posible pudo comprobarlo contra nuevas observaciones hasta que se llegó a un acuerdo satisfactorio.
Kepler concluyó que la órbita de Marte era una elipse con el Sol en uno de sus focos (un resultado que cuando se extiende a todos los planetas que ahora se llama "Primera Ley de Kepler"), y que la línea que une el planeta al Sol barrido áreas iguales en tiempos iguales como el planeta describen su órbita ("Segunda Ley de Kepler"), que es el área que se utiliza como una medida de tiempo. Después de que este trabajo fue publicado en Nueva Astronomía ... (Astronomia nova, ..., Heidelberg, 1609), Kepler encontró las órbitas de los otros planetas, estableciendo así las dos leyes para ellos también. Ambas leyes se refieren al movimiento del planeta al Sol; el Copernicanismo de Kepler fue crucial para su razonamiento ya sus deducciones.
El proceso real de cálculo para Marte fue inmensamente laborioso - hay cerca de mil hojas en el folio de la aritmética - y el propio Kepler se refiere a esta obra como "mi guerra con Marte ', pero el resultado fue una órbita que está de acuerdo con los resultados modernos tan exactamente que la comparación tiene que tomar en cuenta los cambios seculares en la órbita desde la época de Kepler.
Error observacional
Era fundamental el método de comprobación de las posibles órbitas con las observaciones que tienen da una idea de lo que debería ser aceptado como un acuerdo adecuado de Kepler. De esto surge el primer uso explícito del concepto de error de observación. Kepler pudo haber adeudado esta noción, al menos en parte a Tycho, que hizo los controles detallados sobre el rendimiento de sus instrumentos (véase la biografía de Brahe).
Óptica, y la nueva estrella de 1604
El trabajo sobre Marte se completó esencialmente por 1605, pero hubo demoras en el libro publicado. Mientras tanto, en respuesta a las preocupaciones acerca del diferente diámetro aparente de la Luna cuando se observa directamente y cuando se observa el uso de una cámara oscura, Kepler hizo algunos trabajos sobre óptica, y se le ocurrió la primera teoría matemática correcta de la cámara oscura y la primera explicación correcta del funcionamiento del ojo humano, con una imagen invertida formada en la retina. Estos resultados fueron publicados en suplementos, en la parte óptica de la astronomía (Ad Vitellionem paralipomena, quibus Astronomiae pars traditur optica, Frankfurt, 1604).
También escribió sobre la Nueva Estrella de 1604, ahora generalmente llamada 'supernova de Kepler', rechazando numerosas explicaciones, y comentando en un punto que por supuesto esta estrella podría ser sólo una creación especial ' (En la nueva estrella, De stella nova, Praga, 1606, Capítulo 22, KGW 1, p. 257, línea 23).
Tras el uso de Galileo del telescopio en el descubrimiento de las lunas de Júpiter, publicado en su Mensajero Sideral (Venecia, 1610), a la que Kepler había escrito una respuesta entusiasta (1610), Kepler escribió un estudio de las propiedades de las lentes (el primer tipo de trabajo sobre óptica) en la que presentó un nuevo diseño de telescopio, usando dos lentes convexas (Dioptrice, Praga, 1611). Este diseño, en el que se invierte la imagen final, tuvo tanto éxito que ahora se conoce generalmente no como un telescopio Kepler sino simplemente como el telescopio astronómico.
Dejando a Praga para Linz
Los años de Kepler en Praga fueron relativamente pacífica, y científicamente muy productivos. De hecho, incluso cuando las cosas iban mal, nunca parece haber permitido que las circunstancias externas para impedirle seguir adelante con su trabajo. Las cosas empezaron a ir muy mal a finales de 1611. Kepler tuvo que abandonar Praga. Él y el resto de sus hijos se trasladaron a Linz (ahora en Austria).
Matrimonio y los barriles de vino
Kepler parece haberse casado con su primera esposa, Barbara, por amor (aunque el matrimonio fue arreglado a través de un intermediario). El segundo matrimonio, en 1613, era una cuestión de necesidad práctica; que necesitaba a alguien para cuidar a los niños. La nueva esposa de Kepler, Susana, tuvo un curso intensivo en el carácter de Kepler: la carta dedicatoria del libro resultante explica que en las celebraciones de la boda, Kepler se dio cuenta de que se requeria estimar los volúmenes de los barriles de vino y comenzó a preguntarse cómo podría funcionar.
El resultado fue un estudio de los volúmenes de sólidos de revolución (Nueva Stereometry de barriles de vino ..., Nova stereometria doliorum ..., Linz, 1615) en la que Kepler, basándose en el trabajo de Arquímedes, usó una resolución en ' indivisibles ". Este método fue desarrollado posteriormente por Bonaventura Cavalieri (c 1598 -. 1647) y es parte de la ascendencia del cálculo infinitesimal.
La armonía del mundo.
La principal tarea de Kepler como Matemático Imperial era escribir tablas astronómicas, con base en las observaciones de Tycho, pero lo que realmente quería hacer era escribir La Armonía del Mundo, prevista desde 1599 como un desarrollo de su Misterio del Cosmos. Este segundo trabajo sobre la cosmología (libri Harmonices mundi V, Linz, 1619) presenta un modelo matemático más elaborado que el anterior, aunque los poliedros están todavía allí.
Las matemáticas en este trabajo incluyen el primer tratamiento sistemático de mosaicos, una prueba de que hay sólo trece poliedros convexos uniformes (los sólidos de Arquímedes) y el primer relato de dos poliedros regulares no convexos (todos en el Libro 2). La Armonía del Mundo también contiene lo que ahora se conoce como "la tercera ley de Kepler, que para dos planetas la relación de los cuadrados de sus periodos será la misma que la relación de los cubos de los radios medios de sus órbitas.
Desde el principio, Kepler había buscado una norma relativa a los tamaños de
las órbitas a los períodos, pero no había ninguna serie lenta de pasos hacia
esta ley, ya que había sido hacia los otros dos. De
hecho, aunque la tercera ley juega un papel importante en algunos de los tramos
finales de la versión impresa de la armonía del mundo, no fue en realidad
descubierta hasta que el trabajo estaba en prensa. Kepler hizo revisiones de último
minuto.
Él mismo cuenta la historia del éxito final:
... Y si quieres el momento exacto en el tiempo, que fue concebido mentalmente el 8 de marzo de este año un mil seiscientos dieciocho, pero sometido al cálculo de una manera ligera, y por lo tanto la rechaze como falsa, y finalmente regreso al 15 de mayo y adopto una nueva línea de ataque, irrumpieron en la oscuridad de mi mente. Tan fuerte fue el apoyo de la combinación de la obra, de diecisiete años sobre las observaciones de Brahe y el presente estudio, que conspiraron juntos, que al principio creí que estaba soñando, y asumiendo mi conclusión entre mis premisas básicas. Pero es absolutamente cierto y exacto que "la proporción entre los tiempos periódicos de cualquiera de los dos planetas es precisamente la proporción sesquialterate de sus distancias medias ..."
... Y si quieres el momento exacto en el tiempo, que fue concebido mentalmente el 8 de marzo de este año un mil seiscientos dieciocho, pero sometido al cálculo de una manera ligera, y por lo tanto la rechaze como falsa, y finalmente regreso al 15 de mayo y adopto una nueva línea de ataque, irrumpieron en la oscuridad de mi mente. Tan fuerte fue el apoyo de la combinación de la obra, de diecisiete años sobre las observaciones de Brahe y el presente estudio, que conspiraron juntos, que al principio creí que estaba soñando, y asumiendo mi conclusión entre mis premisas básicas. Pero es absolutamente cierto y exacto que "la proporción entre los tiempos periódicos de cualquiera de los dos planetas es precisamente la proporción sesquialterate de sus distancias medias ..."
(Harmonice mundi libro 5, capítulo 3, trad. Aiton, Duncan y Campo, p. 411).
Juicio por Brujería
Mientras que Kepler estaba trabajando en su Armonía del Mundo, su madre fue acusada de brujería. Se contó con la ayuda de la facultad legal de Tübingen. Katharina Kepler fue finalmente puesto en libertad, al menos en parte, como resultado de objeciones técnicas derivadas de la insuficiencia de las autoridades a seguir los procedimientos legales correctos en el uso de la tortura. Los documentos que sobreviven son escalofriantes. Sin embargo, Kepler continuó trabajando. En el coche, en su viaje a Württemberg para defender a su madre, que leyó un trabajo sobre teoría de la música de Vincenzo Galilei (c.1520 - 1591, el padre de Galileo), a la que hay numerosas referencias en La Armonía del Mundo.
Tablas Astronómicas
Cálculo de las tablas, el negocio normal para un astrónomo, siempre involucrado aritmética pesado. Kepler fue consecuencia encantado cuando en 1616 se encontró con la obra de Napier sobre logaritmos (publicada en 1614). Sin embargo, Mästlin le dijo rápidamente primero que era indecoroso para un matemático serio regocijarse sobre una mera ayuda para el cálculo y la segunda que era prudente confiar en los logaritmos porque nadie entendía cómo funcionaban.
(Se hicieron comentarios similares acerca de las computadoras a principios de
1960)
La respuesta de Kepler a la segunda
objeción fue publicar una prueba de cómo funcionaban los logaritmos, basado en
una fuente impecablemente respetable: mesas de Euclides Elementos libro 5.
Kepler calculados de ocho cifras logaritmos, que fueron
publicadas con las Tablas Rudolphine (Ulm, 1628). Las
tablas astronómicas utilizan no sólo las observaciones de Tycho, sino también
las dos primeras leyes de Kepler. Todas
las tablas astronómicas que hicieron uso de las nuevas observaciones eran
exactas durante los primeros años después de la publicación.
Lo extraordinario de las tablas de Rudolphine era que ellos demostraron ser
precisa en las últimas décadas. Y
a medida que los años montados arriba, la exactitud continuada de las mesas
fue, naturalmente, visto como un argumento para la corrección de las leyes de
Kepler, y por tanto para la corrección de la astronomía heliocéntrica. Cumplimiento
de Kepler de su tarea oficial aburrido como Matemático Imperial llevó a la
realización de su deseo más querido, para ayudar a establecer el
copernicanismo.
Wallenstein
En el momento en que las tablas de Rudolphine se publicaron Kepler, de hecho, ya no trabajaba para el emperador (que había dejado Linz en 1626), pero con Albrecht von Wallenstein (1583-1632), uno de los pocos líderes militares exitosos en la Trigésima Guerra Años (1618-1648).
Wallenstein,
como el emperador Rodolfo, espera que Kepler les de consejos basados en la
astrología.
Kepler tenía, naturalmente, que obedecer, pero señala repetidamente que él
no cree que las predicciones precisas se pueden hacer. Como
la mayoría de la gente de la época, Kepler aceptó el principio de la
astrología, que los cuerpos celestes pueden influir en lo que pasó en la Tierra
(los ejemplos más claros es el Sol causando las estaciones y la Luna las
mareas), pero como copernicano no creía en la realidad física de las constelaciones.
Su astrología se basa sólo en los ángulos entre las posiciones de los
cuerpos celestes ('aspectos astrológicos'). Él
expresa el desprecio absoluto por los complicados sistemas de la astrología
convencional.
Las tres leyes de Kepler
Durante su estancia con Tycho le fue imposible acceder a los datos de
los movimientos aparentes de los planetas ya que Tycho se negaba a dar
esa información. Ya en el lecho de muerte de Tycho y después a través de
su familia, Kepler accedió a los datos de las órbitas de los planetas
que durante años se habían ido recolectando. Gracias a esos datos, los
más precisos y abundantes de la época, Kepler pudo ir deduciendo las
órbitas reales planetarias.
Afortunadamente, Tycho se centró en Marte,
con una órbita elíptica muy acusada. De otra manera le hubiera sido
imposible a Kepler darse cuenta de que las órbitas de los planetas eran
elípticas. Inicialmente, Kepler intentó la circunferencia por ser la más
perfecta de las trayectorias, pero los datos observados impedían un
ajuste correcto, lo que entristeció a Kepler, ya que no podía saltarse
un pertinaz error de ocho minutos de arco. Kepler comprendió que debía
abandonar la circunferencia, lo que implicaba abandonar la idea de un
"mundo perfecto".
De profundas creencias religiosas, le costó llegar a
la conclusión de que la tierra era un planeta imperfecto, asolado por
las guerras. En esa misma misiva incluyó la cita clave: "Si los planetas
son lugares imperfectos, ¿por qué no han de serlo las órbitas de las
mismas?". Finalmente utilizó la fórmula de la elipse, una rara figura
descrita por Apolonio de Pérgamo en una de las obras salvadas de la destrucción de la biblioteca de Alejandría. Descubrió que encajaba perfectamente en las mediciones de Tycho.
Había descubierto su primera ley, la primera ley de Kepler:
Los planetas tienen movimientos elípticos alrededor del Sol, estando éste situado en uno de los 2 focos que contiene la elipse.
Después de ese importante salto, en donde por primera vez los hechos
se anteponían a los deseos y los prejuicios sobre la naturaleza del
mundo. Kepler se dedicó simplemente a observar los datos y sacar
conclusiones ya sin ninguna idea preconcebida. Pasó a comprobar la
velocidad del planeta a través de las órbitas llegando a la segunda ley:
Las áreas barridas por los radios de los planetas son proporcionales al tiempo empleado por estos en recorrer el perímetro de dichas áreas.
Durante mucho tiempo, Kepler sólo pudo confirmar estas dos leyes en
el resto de planetas. Aún así fue un logro espectacular, pero faltaba
relacionar las trayectorias de los planetas entre sí. Tras varios años,
descubrió la tercera e importantísima ley del movimiento planetario:
El cuadrado de los períodos de la órbita de los planetas es proporcional al cubo de la distancia promedio al Sol.
Esta ley, llamada también ley armónica, junto con las otras leyes, permitía ya unificar, predecir y comprender todos los movimientos de los astros.
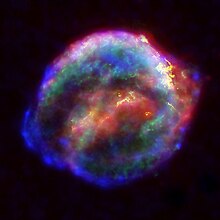
SN 1604: La estrella de Kepler
Restos de la estrella de Kepler, la supernova SN 1604. Esta imagen ha sido compuesta a partir de imágenes del Telescopio espacial Spitzer, el Telescopio Espacial Hubble y el Observatorio de Rayos X Chandra.
El 17 de octubre de 1604 Kepler observó una supernova en la Vía Láctea, nuestra propia Galaxia, a la que más tarde se le llamaría la estrella de Kepler. La estrella había sido observada por otros astrónomos europeos el día 9 como Brunowski en Praga (quién escribió a Kepler), Altobelli en Verona y Clavius en Roma y Capra y Marius en Padua. Kepler inspirado por el trabajo de Tycho Brahe realizó un estudio detallado de su aparición. Su obra De Stella nova in pede Serpentarii («La nueva estrella en el pie de Ophiuchus») proporcionaba evidencias de que el Universo
no era estático y sí sometido a importantes cambios. La estrella pudo
ser observada a simple vista durante 18 meses después de su aparición.
La supernova se encuentra a tan solo 13 000 años luz de nosotros. Ninguna supernova posterior ha sido observada en tiempos históricos dentro de nuestra propia galaxia. Dada la evolución del brillo de la estrella hoy en día se sospecha que se trata de una supernova de tipo I.